The role of power in aeronautics is an important and overlooked topic. We hope that you find the concept of power an interesting and useful tool in understanding the physics of flight and the behavior of an airplane in flight. We will first briefly describe drag.
Drag
In aeronautics, the discussions almost exclusively focus on drag. It is a subject ingrained in all pilots. Power is seldom mentioned except for engines. Even the classic aeronautics textbooks do not discuss the power associated with flight. You will see that it is easy to calculate the functional form of power, though we will be brief so that the ideas are easier to understand. The details can be easily found elsewhere [1]. Drag on the other hand is not easy to calculate but drag is related to power which is easy to calculate by the speed. Drag is equal to power divided by speed.
Drag, by its nature, is a negative concept. It is a retarding force that fights the wishes of the pilot. Designers work to minimize it. Induced drag is the drag associated with lift. It expresses the work performed to produce lift and can never be reduced to zero. Minimizing induced drag merely improves the efficiency of lift.
Another problem with drag is that its effect varies with speed. The engine power required to overcome a certain drag is proportional to the speed. Take two different airplane types; one is going 50% faster than the other, and both are overcoming the same drag. The faster airplane will require 50% more power to overcome the same drag as the other airplane. The effect of drag means little without knowing the speed.
Power
Power is simply the rate of doing work. A pump lifting water from a well is doing work and requires a certain power. If the height the pump had to lift the water or the rate the water had to be pumped, were doubled, the amount of power needed would be doubled. An airplane has no drag meter but power is simply the rate of fuel consumption.
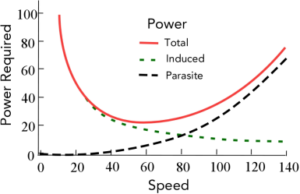
For an airplane, there are two sources of power consumption. These are induced power and parasite power. Induced power is the rate energy is put into the air to produce lift. Parasite power is the power loss due to the air colliding with parts of the airplane. The total power requirement for flight is the sum of the induced power and the parasite power. The three powers are plotted in Figure 1. The total power is called the Power Curve and gives the power necessary for straight-and-level flight as a function of speed.
For reasons discussed below, induced power is proportional to one over the speed (1/S) of the airplane through the air. The slower one goes; the more power is required. That is because lift becomes less efficient at slow speeds. The total power curve on the low-speed side of the minimum power requirement is referred to as the “back side of the power curve”.
Samuel Langley, one of the early investigators of flight at the time of the Wright brothers, claimed that the faster one went, the less power was required. Needless to say, that idea was scoffed at. Well, he was right.
In the early days, the engines were so underpowered that they were all flying on the backside of the power curve. Langley built an unmanned model of an airplane that included a steam-powered engine. In 1891, his model flew for 3/4 of a mile before running out of fuel, Figure 2.
Parasite power
Our discussion begins with parasite power because the physics is simple and has a smaller impact on understanding the physics of flight. Parasite power is due to the collision of air with the airplane. This is proportional to the amount of energy transferred to the airplane by an air molecule times the rate of such collisions. The energy of the collision of an air molecule with the airplane is equal to the kinetic energy which is equal to the speed squared of the airplane or the air molecule. The rate molecules collide with the airplane is proportional to the speed times the density of the air. This gives another power of speed. (Note that it makes no difference if the air strikes the wing as in a wind tunnel or the wing strikes the air as in flight.) Thus, parasite power is proportional to the speed cubed times the density:
Parasite Power equals speed cubed times air density
Parasite power is shown in Figure 1. At cruise speed, parasite power dominates an airplane’s power requirement. This should be clear by the high-speed side of the power curve.
Parasite power is proportional to the speed cubed. This is the limiting factor in the top speed of an airplane where parasite power dominates. For an existing airplane to double its top speed the engine power would need to be increased by a factor of 8! In designing a faster airplane, it is much more important to reduce the parasite power (or parasite drag) requirement than to increase the engine’s power. On the other hand, a larger engine shortens the takeoff distance and increases the rate of climb.
Induced Power
As a reminder, the lift on a wing is proportional to the rate air is accelerated perpendicular to the direction of travel times the velocity of that air. This is true for all wings.
Lift on a wing = rate air is accelerated times the speed of that air.
As explained in the Lift Details:
- The amount of air accelerated is proportional to the density of the air and the speed of the airplane through the air.
- The speed of the accelerated air is proportional to the speed of the airplane times and the effective angle of attack. Lift is plotted schematically in Figure 3.
- From Newton’s second law of motion, we have shown that lift is equal to the rate of change of the momentum of the accelerated air (momentum = mv).
Induce power is equal to the rate of change of the kinetic energy of the accelerated air (KE =1/2 mv^2). Thus, we have:
Induced power = rate of air accelerated times the speed of that air squared
We have shown that parasite power goes as the speed of the airplane cubed. So now we address how the induced power goes as the speed. Let’s assume that the speed of the airplane is reduced to half. The amount of air accelerated is now halved. The vertical velocity of that air must be doubled by increasing the angle of attack to maintain a constant lift. Since the induced power goes as the amount of air diverted times the vertical speed of that air squared, we have ½ times 2 times 2 = 2. Thus, to go half the speed the induced power doubles. This gives the famous result that:
Induced power goes as one over the speed (1/S) of the airplane
We have that the induced power varies as one over the speed on the back side of the power curve. Induced power is the power the engine must provide to produce lift. With a little contemplation, one can derive that the angle of attack goes as one over the speed squared. Because the angle of attack increases faster than induced power with decreasing speed, the airplane will stall before it reaches the point of insufficient power.
Drag and Power
Before we go on with some applications of our knowledge of power, let’s revisit the relationship between power and drag. At a constant altitude, we have shown that Induced power goes as 1/S and parasite power goes as S3. So, for any airplane, we can write:
Power = a/S +bS3
Where “a” and “b” are constants determined in a flight test of the airplane. Since drag is just power divided by speed we have:
Drag = a/S2 + bS2
Where “a” and “b” are the same constants as in the expression for the power. So, if the power is determined, the drag is also determined.
Some Applications
Increased load
Assume you are flying along in your Cessna 172 and Scotty (from the starship Enterprise) beams down two well-fed Sumo wrestlers, doubling the airplane’s weight. Maintaining the original speed and altitude, the rate air is accelerated down remains unchanged so the vertical velocity of the air must be doubled. Because induced power is proportional to the vertical velocity of the air squared, doubling the load increases the induced power by a factor of 4. Thus, we have:
Induced Power is proportional to the load squared
That is why so much effort and expense is put into making an airplane as light as possible. So, if you buy the last ticket for a long flight thinking that you aren’t going to use any more fuel, you’re wrong. You will cause the consumption of more fuel than anyone else on the airplane.
Increased altitude
Airplanes fly at high altitudes to reduce fuel consumption. At 36,000 feet the air density is ¼ that at sea level. It is easy to show that induced power increases as one over the air density. Thus, the induced power is increased by a factor of 4.
At 36,000 feet Induced power increases by a factor of 4 and parasite power decreases by a factor of 4. Since airplanes fly at speeds where parasite power dominates, it is more efficient to fly high.
As an airplane climbs in altitude, induced power increases and so the excess energy (power not necessary for lift and available for climb) decreases, as does the rate of climb. At some altitude, total power equals an engine’s total output. That is the absolute ceiling of the craft. At that point, the power requirement is almost all induced power and some of the lift is due to the airplane “hanging” on the engine.
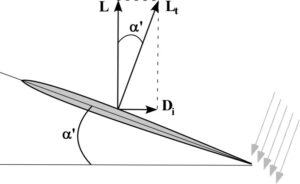
Lift and Induced Drag
We said above that the accelerated air that produces lift goes straight down for straight-and-level flight. Since the wing is tilted back at the effective angle of attack, the total lift vector, Lt, is tilted back at the same angle. This is illustrated in Figure 4. The vertical component of the total lift vector is the lift on the wing, L, and the horizontal component is the induced drag, Di. Since the total lift vector has a rearward tilting angle, Newton’s 3rd law says that the force accelerating the air down must have a forward component. Typical values of the effective angle of attack are on the order of 2-5 degrees so the effect of the air having a slight forward direction can be minor. The effective angle of attack in Figure 4 is greatly exaggerated for clarity. The point is, that the induced drag is just the rearward component of the total lift vector. The only way to make induced drag zero would be to make the angle of attack zero. But then there would be no lift.
Take away
The important points to remember are:
- Power is the rate of doing work
- Induced power goes as:
- 1/speed
- Load squared
- 1/air density
- Parasite power goes as:
- Speed cubed
- Air density
We hope that we have made it clear the importance of a true understanding of flight and that one sees the handicap in understanding when hobbled by misconceptions.
One might be interested in the debunking of the propeller spiraling slipstream myth. It is a fantasy and a clear violation of Newton’s first and third laws.
References
David F. Anderson and Scott Eberhardt. Understanding Flight, 2nd ed. (McGraw-Hill, 2010).