Coanda and Not Bernoulli
Bernoulli Principle
The Bernoulli equation is valid in a closed environment, such as a pipe, where energy cannot be added or subtracted. Even there, it is only an approximation due to energy loss because of friction and viscosity. Aeronautical engineers also use it to calculate pressures and airflow around a wing. But it is not a physical description of lift. It is only a calculation tool. See Aeronautics and the Bernoulli Equation.
A key point to understand is that unconfined, faster-moving air has the same static pressure as the surrounding environment. Except for the venturi, none of the phenomena associated with the Bernoulli principle have anything to do with the Bernoulli principle. We have divided the phenomena into two categories. The first are those due to the Coanda effect, typified by a fluid following a convex surface. The Magnus effect is also discussed which is an application of the Coanda effect on rotating objects. The second is due to what we have called, for lack of a better idea, the “draft effect”. This latter effect is typified by the draft of a chimney drawing air into a fireplace.
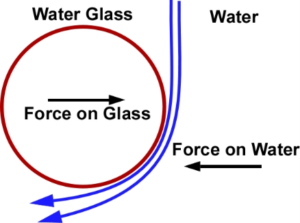
Coanda Effect
The Coanda effect states that a fluid or gas stream will hug a convex contour when directed at a tangent to that surface. This was discovered in the 1930s by a Romanian named Henri-Marie Coanda. He did many experiments while riding in the front of a railroad train. Figure 1 shows an example of the Coanda effect. A glass is gently moved into a stream of water. Instead of the water pushing the glass out of the stream, it draws it in. Because of viscosity, a thin layer of water adheres to the glass. Just above that layer, the water moves a little faster, and so on, until the full speed of the flow is reached. This change in flow rate causes a sheer force that bends the water. This puts a force on the water, and by Newton’s third law, an equal and opposite force on the glass. The net result is the transfer of momentum. Momentum transfer creates lift on a wing but not due to the Coanda Effect. Momentum transfer is like the recoil force of a garden hose. The transfer of momentum to the water leaving the hose produced a recoil force on the hose.
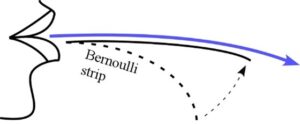
The “Bernoulli Strip”.
The Bernoulli strip is a thin strip of paper that one blows across the top as in Figure 2. The strip lifts up. The faulty logic is that since your breath is moving fast across the paper it has a lower static pressure and lifts the strip. The reality is this is an example of the Coanda Effect and momentum transfer. The air is bent down around the paper which causes a lifting force on the strip.
If one tries the Bernoulli strip, notice that it never comes up flat. That is because there has to be a downward bend to produce lift. If the Bernoulli explanation were true, the lower pressure would bring the strip up flat.
A clever variation on the Bernoulli strip is the Coanda Flying Sauser shown in Figure 3. If one Googles “Coanda Flying Sauser” you will see some very clever designs.
Ping Pong Ball in a jet of air.
A common “demonstration” of the Bernoulli principle is the confinement of a ping pong ball in a jet of air such as the exhaust of a vacuum cleaner (Figure 4). When the ball is near the center of the jet of air, the flow around the ball is essentially equal on both sides. Thus, there is no lateral force on the ball. When the ball is near the edge of the flow, more air is turned by the side of the ball nearer the center of the flow. So, there is a restoring force, again due to momentum transfer.
An eye-catching example of this phenomenon is shown in Figure 5. Here the ping pong ball is suspended in a thin jet of water.
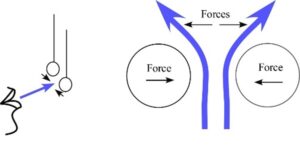
Blowing between two suspended ping pong balls.
In this demonstration two ping pong balls are suspended on strings, Figure 6. The space between them reduces when one blows air between them. Of course, the faulty logic is that one’s breath has a lower static pressure like with the Bernoulli strip. Again, it is a simple momentum transfer. This demonstration is sometimes done with two empty soda cans.
Curve Ball.
The curveball is another common misapplication of the Bernoulli principle. Image “A” in Figure 7 is the drag force on a non-spinning baseball moving to the left. The airflow is in the rest of the frame of the baseball. The air flows uniformly around the ball and eventually separates from the ball. The more it flows around the ball the less the drag force.
The common myth associated with the curveball is when the ball is spinning, as in image “B”. The bindings on the ball drag air around the ball. The Bernoulli idea is that on top of the ball, the spinning air is slowing down the air above the ball thus increasing the pressure, while the reverse is happening below the ball. Thus, there is a downward force changing the trajectory of the ball. There is such a force but it has nothing to do with Bernoulli.
Image “C” shows the actual airflow around the spinning ball. The spin on the top of the ball reduces the energy in the air near the ball causing it to stall (separation) earlier. The ball’s spin on the bottom adds energy to the air causing a delayed stall. The result is an asymmetric stall that gives an upward momentum transfer and a downward force. Below you will see that some call the effect that curves the ball the Magnus effect.
As a note of interest, dimples on a golf ball are important because they help create turbulence in the layer of air around the ball which reduces drag and therefore makes the ball fly farther. This is much like the vortex generators on a wing. It is widely believed that a golf ball without dimples would fly about half the distance of a golf ball with dimples because of this technology.
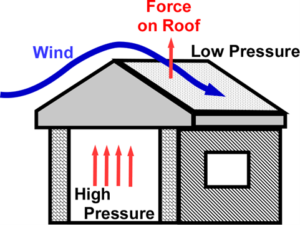
Hurricane taking off a roof
When a hurricane wind blows over the roof of a house, Figure 8, it sometimes takes off the roof. Often the given reason is that the pressure is lower above the roof than inside the house. And of course, every explanation attributes the phenomenon to the air going faster over the roof, and we all know that air with higher speed has a lower pressure due to the Bernoulli effect. We put that statement in to see if you were still awake. Of course, we know this Bernoulli explanation is wrong! The house is just like a giant ping pong ball and the force is due to the Coanda Effect and momentum transfer.
Magnus Effect
There are many applications of the physics of the curve ball. The effect is called the Magnus Effect which is an application of the Coanda effect on rotating objects. It is applied to ship sails, model airplanes, and other applications.
Isaac Newton was the first scientist to describe the Magnus effect and its possible causes in 1671. However, it was named after the German physicist Heinrich Gustav Magnus, who described the effect in 1852.
Internet sources wrongly define the Magnus Effect as:
“The Magnus Effect is, in fact, a special case of Bernoulli’s principle (Coanda Effect) which states that an increase in the speed of a fluid simultaneously occurs with a decrease in pressure….” More falsehoods! Sigh.
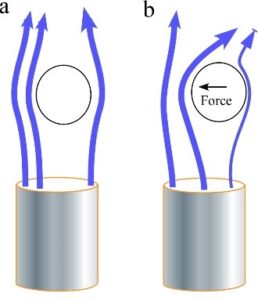
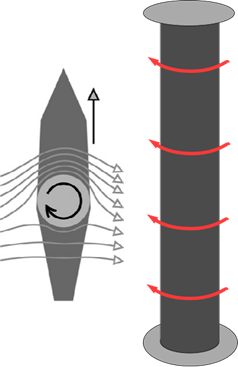
Figure 9a & 9b shows Magnus sails. These are rotating cylinders on a boat or ship to provide some propulsion.
The Magnus effect is real and has received significant effort and funding. Almost without exception, it is explained by applying the Bernoulli principle. With some effort, one can find a non-Bernoulli explanation of the Magnus Effect on the internet but it’s often very confusing. One should note that the airflow in the figure is very much like the airflow of the curve ball.
Another example of the Magnus Effect is the trajectory of a bullet in a crosswind. Look at Figure 7 – Curveball image B – and imagine the ball is a receding bullet with a counter-clockwise spin. With the wind coming from the left a downward force is put on the bullet and the bullet will hit low. A wind from the right will cause the bullet to go high. You can guess how this phenomenon is explained in the literature.
The video to the right provides a good explanation and demonstration of the Magnus Effect.
“Draft Effect”
The fireplace is a simple demonstration of a phenomenon that will be used to explain several faux Bernoulli explanations. In Misconception #1, we made it clear that faster-moving air does not have a lower pressure if not confined. The heat from the fire warms the air in the chimney. The air becomes less dense and rises in the chimney thus drawing in air from the room, Figure 10. The rising air in the chimney lowers the pressure in the fireplace. This draws in air from the room that is at ambient pressure. The rising air also transfers momentum to the surrounding air giving it an upward velocity enhancing the draw. For lack of a better name, we call this the “draft effect”.
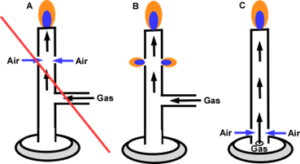
Bunsen Burner
Bunsen burners are used in almost every chemistry lab in the world. Figure 11 shows three drawings of the Bensen burner. Drawing “A” came from the internet in a discussion of how a Bunsen burner works. The idea is that the gas moving fast past the air holes would draw in the air. Drawing “B” is what would happen if one built Bunsen burners like that. The “air holes” would be leaks and there would be three flames.
Drawing “C” of Figure 11 shows how a Bunsen burner really works. There is a high-speed jet at the bottom with the air vents nearby. Like in the fireplace, the jet of gas accelerates the air up which draws in air from the vents placed near the jet.
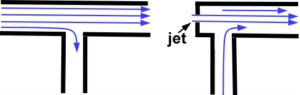
Figure 12 shows a detail of airflow in a tube with a smaller tube attached at 90 degrees. In the first configuration, the gas splits at the union. In the second configuration, a high-speed jet has been added. Now the gas is drawn from the smaller tube.
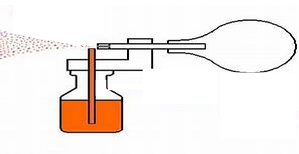
Atomizers
Explanations of how atomizers work often invoke the Bernoulli principle. Again, the physics is that of the fireplace as demonstrated in Figure 13. High-speed air from the squeezed bulb blows across the end of the tube in the liquid. The high velocity of the air from the bulb transfers momentum to the surrounding air or liquid causing it to move in the same direction. Since the air from the bulb is not confined, it cannot have a lower pressure than the surrounding air. Often the atomizer tube is placed with a slight upward angle. This enhances the draw. Here is another example of the draft effect.
Takeaway.
There are many phenomena mistakenly associated with the Bernoulli principle. It’s safe to say, that except for the venturi and a few others in fluid dynamics, none have anything to do with Bernoulli. These false phenomena are roughly divided into two groups: those related to the fireplace phenomenon and those that consist of flow over a surface. The second group is due to the Coanda Effect which is real science. Had people understood that unconfined, faster-flowing fluids do not have a lower pressure, we would be touting Coanda rather than Bernoulli. From the Broadway play (not the movie) The Best Little Whore House in Texas we have: “They’re peeing on your boots and telling you it’s rain”. So, when someone tries to explain a phenomenon with the Bernoulli principle keep an eye on your boots.