How Lift is Changed
In Lift on a Wing, we presented the lift of any wing in flight. What was presented applies to an airplane at a constant attitude, speed, and load. Now we will explain how a wing adapts to the constantly changing environment of flight.
A wing accelerates air perpendicular to the flight path. Thus, according to Newton’s first law, there must be a force on that air. Newton’s third law states that there must be an equal and opposite force on the wing. That’s lift.
Newton’s second law states that force is equal to the change in momentum of the air. As explained in Lift on a Wing, the lift on a wing is proportional to the rate at which air is accelerated times the speed of that air. This is true for all wings in flight. This fact is simple, elegant, and doesn’t involve the shape of the wing or any other plausible falsehoods.
In Lift on a Wing, we stated that a Cessna 172 accelerates tons of air per second. Let’s do a back-of-the-envelope calculation for an airplane that weighs one metric ton and accelerates air down at 3 m/s. That’s about 7 mph. We have said that lift, L, is equal to the rate air is accelerated, R, times the speed of that air, V. This is written:
L=RV
L= the weight of the airplane (1,000 kg) times gravity (9.8m/s2). The 9.8 m/s2 is the acceleration of gravity that converts kg into force.
V = 3m/s
Rearranging L=RV to solve for R, we get:
R=L/V, hence
R=(9,800kgm/s2)/ (3 m/s)
R = 3.267 tons/sec
The power necessary to accelerate this air and produce lift is 36 hp. Quite a reasonable number considering the airplane may be using 150 hp.
We can now express lift as a function of air density, speed of the wing through the air, and effective angle of attack (eAoA). Do you remember the effective angle of attack? The eAoA is measured from the orientation into the wind that produces zero lift.
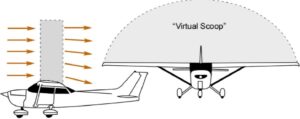
Let’s look at two factors of lift. First, the amount of air accelerated. Second, the speed of the accelerated air. To understand the amount of air a wing interacts with to produce lift, we must first imagine the wing as a scoop, as shown in Figure 1. The amount of air intercepted does not depend on the angle of attack or the load on the wing. The amount of air intercepted is proportional to air density and the airplane’s speed. The dependence on airspeed should be obvious. The faster the airplane travels, the more air it intercepts. It’s the same with density. The denser the air, the more air (mass) that is intercepted. So, we have:
The amount of air intercepted is proportional to the airspeed and air density.
Although the scoop image may seem contrived, there is a good mathematical justification. And, we find it to be a useful image to help people understand lift.
We now address how the vertical velocity of the air is changed. Refer to Figure 2. Image “a” depicts a wing traveling at a certain speed, S, and with a certain effective angle of attack (eAoA), α. This yields a certain vertical velocity (Vv). Image “b” shows the same wing with the eAoA (α doubled. You see that the vertical velocity has also doubled. Image “c” shows the result of doubling the wing’s speed. The vertical velocity has also doubled. This gives us the results that:
The velocity of the air is proportional to the effective AoA and the speed of the wing.
Note: The drawing in Figure 2 is in the rest frame of the wing, not the rest frame of the air that we have used elsewhere. This rest frame is used for clarity. The vertical velocity is what would be seen in the rest frame of the air.
Figure 3 is a diagram of the lift for any wing. Lift equals the amount of air accelerated times the speed of that air. The rate air is accelerated is proportional to the air density and the speed of the wing. The speed of the accelerated air is proportional to the speed of the wing and the effective angle of attack. This is true for any wing, including an inverted wing.
Figure 3 is the lift on a wing of any shape. It allows us to determine the flight characteristics under any condition. For an airplane in straight and level flight, where the lift must equal the weight of the airplane, we offer the following as examples of the utility of this figure:
- Many know that lift on a wing goes as the airplane’s speed squared. This is true. By examining Figure 3, one sees that both the rate the air is accelerated and the speed of the accelerated air are proportional to the speed of the wing.
- An increase in altitude means a reduction in air density: either the effective AoA or speed must be increased. If one climbs to a higher altitude at a fixed speed, the effective AoA would have to increase. If the air density were halved, the effective AoA would have to be doubled.
- Increase in speed: go to a higher altitude or decrease the effective angle of attack.
- Decrease load (burn off fuel): gain altitude, reduce speed, or reduce the effective AoA (note: A Boeing 747 at gross weight for a trans-ocean flight is 45% fuel by weight). This will be discussed in Step and Cruise Climb.
By removing the misconceptions of flight and employing Newton’s three laws and logic, we now understand the truth of flight rather than relying on falsehoods. We have also demonstrated the power of true understanding. Figure 3 gives the lift on any wing at any speed, effective angle of attack, and air density. All this without any consideration of the shape of the wing.
Step and Cruise Climb
An airplane will adjust the lift by changing the angle of attack. The large commercial jets on long flights do not have that luxury. For optimum efficiency, the airplane must fly at a defined speed range and with the fuselage directed directly into the oncoming air, that is, at a constant angle of attack. Except for small changes, they are left only with the speed to correct for the reduced load. Given a fixed altitude, they must slow down as the fuel is burned off. At some point, they are allowed to increase their altitude by typically 2,000 feet. This reduces the air density and allows an increase in speed to a range of improved efficiency. This is called a Step Climb.
Ideally, the airplane would fly a slow, continuous climb to reduce the air density to match the continuously decreasing load. This is called a Cruise Climb. The only airplane that was allowed to do this was the Concorde. Because it flew so high, a cruise climb would not be a hazard to other aircraft.
Air Flowing Over the Wing
As we have been taught, lower-pressure air does flow over the top of the wing as shown in Figure 4. This air is drawn in by the reduced pressure that is accelerating air down. This causes the well-known upwash. The velocity of the “flowing air” is caused by the reduced pressure resulting from the production of lift and not the other way around. As previously stated, the pressure and velocity of this air are in no way related by the Bernoulli equation.
Figure 4 also shows the pressure on the top of the wing. The deepest low pressure is near the front of the wing and increases to near ambient pressure at the trailing edge. Although the pressure is reduced over the entire top of the wing, the flowing air must move through an ever-increasing pressure, called an adverse pressure gradient. Thus, as it moves across the wing, it loses speed and energy.
This flowing air is not the cause of lift. First, it does not produce the reduced pressure but is an expression of the reduced pressure, i.e., the reduced pressure causes the flowing air. Second, it has very little mass and energy and is moving in the wrong direction to provide the tons of air that must be accelerated to produce the lift. The flowing air is truly a “red herring” and has been the cause of the confusion for over a century.
The Stall
When the angle of attack becomes too great the wing stalls. So, what is happening? As stated above, as the flowing air moves against the adverse pressure gradient it loses speed and energy. As the angle of attack increases the depth of the maximum low pressure increases and moves forward, and the pressure gradient becomes steeper. This puts more of the wing under an increased adverse pressure gradient. Eventually, the angle of attack is such that the flowing air has zero speed and energy just at the trailing edge. This is the beginning of a stall. At this point, the flowing air does not go past the wing’s trailing edge and the wing continues to develop full lift across its span.
Referring to Figure 5, as the angle of attack increases further, the air exhausts its energy farther from the trailing edge and stops flowing. With no energy, the air nearest the surface separates from the wing. This is called the “separation point”. Because the wing still has a pressure gradient after the separation point, the air behind the trailing edge is drawn in. Thus, there is a reverse flow. Behind the separation point, there is turbulence and no lift. An interesting point is that although the flowing air contributes nothing to the lift on a wing, it is the cause of the stall. If this flowing air were not there, the wing would not have stalled at this point.
Note: One of the problems in discussing flight is the use of the word “vacuum,” which we have avoided. The reduction in pressure above the wing is just a few percent of an atmosphere. The reduction in pressure of a Cessna 172 at sea level is 0.7% of an atmosphere. A person can draw from 0.5% to 0.8% of an atmosphere with their lungs. An F-15 Eagle draws 5.6% of an atmosphere at sea level, and the Airbus A380 has a 7% reduction at sea level. These reductions in pressures can hardly be called a vacuum, which is defined as a space entirely devoid of matter.
Take Away
- Lift on a wing is equal to the rate air is accelerated times the vertical speed of that air.
- The amount of air accelerated is proportional to the airspeed and the density of the air.
- The vertical velocity of the air is proportional to the effective angle of attack (eAoA) and the speed of the wing.
Power is a topic almost completely ignored by aeronautics. You will see that power is a much more useful tool in understanding flight than drag. Drag is a retarding force. Power is fuel flow. Read about Power by clicking the link.
1. David F. Anderson and Scott Eberhardt. Understanding Flight, 2nd ed. (McGraw-Hill, 2010).








